 |
| Časť Mandelbrotovej množiny (Wikipédia) |
Veľa ľudí, ktorí veria, že vesmír a život vznikol božským
zásahom, zvykne tvrdiť, že si nevie predstaviť, ako by niečo také komplikované
mohlo za akýchkoľvek okolností vzniknúť inak, ako zásahom dokonalej mysliacej
bytosti. Musím pripustiť, že toto zmýšľanie je intuitívne a osobne, tiež som
prešiel obdobím, keď som do istej miery podobným spôsobom rozmýšľal. Samozrejme to,
že je niečo intuitívne neznamená, že je to správne. V poslednej
dobe sa po vypočutí podobného tvrdenia zvyknem opýtať, „Počuli ste už niekedy
o Mandelbrotovej množine?“ A na túto otázku mám dobrý dôvod.
 |
| Moja vlastná fotka časti množiny |
Mandlebrotova množina, respektíve jej vizualizácia, dokáže vytvárať extrémne komplexné obrazce a niekedy naozaj až
dych berúce scenérie, pričom ak predkladáme, že vesmír je konečný, Mandelbrotova
množina je hlbšia, je dokázateľne nekonečná. Keď sa človek prvý krát pozrie na
vizualizáciu Mandelbrotovej množiny, často má dojem, že na tvorbu tej malej frakcie
jej skutočnej veľkosti bolo treba pomerne veľkú skupinu dizajnérov. V skutočnosti
celá nekonečná a neprebádateľná Mandelbrotova množina je tvorená riadkom inštrukcií.
 |
| Časť Mandelbrotovej množiny (Wikipédia) |
Samozrejme, táto množina má pramálo spoločné so skutočným vesmírom. Je to ale skvelý príklad, že na to, aby vznikli obrovské a na prvý pohľad ohromujúco
komplexné systémy, nie je nevyhnutne potrebná veľká kreatívna energia, či roky
driny. Úplne stačí pár jednoduchých pravidiel, ktoré sú v našom vesmíre vyjadrené fyzikálnymi
zákonmi.
Pod textom sa nachádzajú dve videá, v ktorých si môžte pozrieť, ako približne mnou ospevovaná Mandelbrotova množina vyzerá:
Cestovanie do vnútra množiny
Rôzne obrazce, ktoré sa dajú v množine nájsť

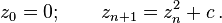
Pekná úvaha. Sú ešte aj iné typy jednoduchých matematických pravidiel, ktoré dávajú vznik konfiguráciám s veľmi vysokou "komplexitou", napríklad celulárne automaty (samozrejme, záleží na tom, čo chápeme pod komplexitou; žiadny obrazec, ktorý sa dá vygenerovať krátkym programom, nemá vysokú Kolmogorovskú zložitosť). Podobne, genetické optimalizačné algoritmy, používajúce jednoduché princípy mutácie, rekombinácie a selekcie, často vyprodukujú pozoruhodne "inteligentné", pripadne "tvorivé" riešenia. Nie je najmenší dôvod tvrdiť, že zložitosť pozorovaná v prírode, prípadne dokonca ľudská inteligencia, nemože byť dôsledkom "neosobných" fyzikálnych zákonov.
OdpovedaťOdstrániť